(2x-5)(2x+5) suma por diferencia

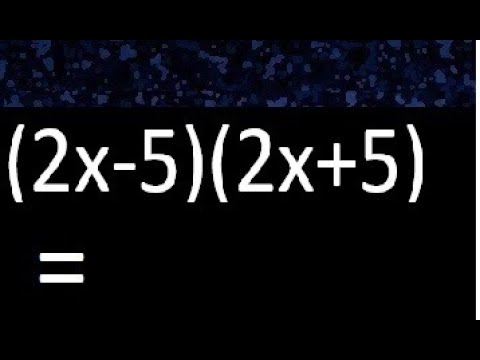
Si p(2x - 1) = x^2 + ax + 6 - a, halla la suma de coeficientes de p(x).

Observa que en el Ejemplo 4b, el signo de cada término cambia cuando la expresión se escribe sin paréntesis. Este es el mismo resultado que habríamos obtenido si hubiéramos utilizado los procedimientos que introdujimos en la Sección 2.5 para simplificar expresiones.

Así, si hay un factor monomial común a todos los términos de un polinomio, podemos escribir el polinomio como el producto del factor común y otro polinomio. Por ejemplo, como cada término de x2 + 3x contiene x como factor, podemos escribir la expresión como el producto x(x + 3). Reescribir un polinomio de esta manera se llama factorización, y se dice que el número x se factoriza "desde" o "fuera de' el polinomio x2 + 3x.

En este libro, restringiremos los factores comunes a monomios formados por coeficientes numéricos que sean enteros y a potencias integrales de las variables. La elección del signo del factor del monomio es una cuestión de conveniencia. Así,

Podemos utilizar la ley distributiva para multiplicar dos binomios. Aunque hay poca necesidad de multiplicar binomios en aritmética, como se muestra en el ejemplo siguiente, la ley distributiva también se aplica a expresiones que contienen variables.

X+5 (x+5 cerebral)

Para ayudarte a memorizar, fíjate primero en que los términos de cada una de las dos fórmulas de factorización son exactamente iguales. A continuación, observa que cada fórmula sólo tiene un signo "menos". La diferencia entre las dos fórmulas radica en la ubicación de ese signo "menos":

Algunas personas utilizan la nemotecnia "SOAP" para ayudar a seguir la pista de los signos; las letras representan el factor lineal que tiene el "mismo" signo que el signo en el centro de la expresión original, a continuación, el factor cuadrático que comienza con el signo "opuesto" de lo que estaba en la expresión original, y, finalmente, el segundo signo dentro del factor cuadrático es "siempre positivo".

Nota: La parte cuadrática de cada fórmula cúbica no se factoriza, así que no pierdas tiempo intentando factorizarla. Sí, a2 - 2ab + b2 y a2+ 2ab + b2 se factorizan, pero eso se debe a los 2 de sus términos medios. Los términos cuadráticos de estas fórmulas de suma y diferencia de cubos no tienen ese "2" y, por tanto, no pueden factorizar.

Cuando te den un par de cubos para factorizar, aplica cuidadosamente la regla adecuada. Por "cuidadosamente" me refiero a "usando paréntesis para controlar todo, especialmente los signos negativos". He aquí algunos problemas típicos:

Suma, diferencia, producto y cociente de dos funciones 143-2.6.1

Gráficamente, es una línea recta. A veces ayuda visualizar lo que sucede, graficando la expresióndivide ambos términos en el numerador por el denominador para obtener (2/5)x + 7/5Grafica la ecuación o función y = f(x) = (2/5)x+ 7/5. Es una ecuación lineal, una recta. Es una ecuación lineal, una línea recta.En la forma estándar de pendiente e intercepto, es una línea con pendiente igual a 2/5 e intercepto y de 7/5. Establece y=0 para obtener el intercepto x (2/5)x=7/5 o 2x=7 o x = 3,5. Traza 2 puntos en los interceptos x e y, (3,5,0) y (0,1,4) y dibuja una línea recta que los conecte y se extienda siempre en ambas direcciones. Si vas verticalmente a cualquier valor de x hacia arriba o hacia abajo de esa gráfica, puedes leer horizontalmente el valor de y, que es igual a la expresión original dada (2x+7)/5.

Cuando se trata de una expresión que tiene una expresión lineal como numerador y un número constante como denominador, basta con dividir cada término del numerador por el número del denominador. La expresión (2x + 7)÷5 es equivalente a (2x/5) + (7/5), que, por cierto, se expresa como una suma.

Producto de la suma y la diferencia de dos términos

Paso 1Para un polinomio de la forma , reescriba el término medio como una suma de dos términos cuyo producto es y cuya suma es.Pulse para más pasos...Paso 1.1Factorice de .Paso 1.2Escriba de nuevo como más Paso 1.3Aplique la propiedad distributiva. Paso 2Factoriza el mayor factor común de cada grupo.Tap for more steps...Paso 2.1Grupa los dos primeros términos y los dos últimos términos.Paso 2.2Factoriza el mayor factor común (MCC) de cada grupo.Paso 3Factoriza el polinomio factorizando el mayor factor común, .